Generating unique integer IDs from strings in MySQL

19 Mar 2010 💬 2

I have an interesting problem, on a data migration project I'm currently working on. I'm importing a large amount of legacy data into Drupal, using the awesome Migrate module (and friends). Migrate is a great tool for the job, but one of its limitations is that it requires the legacy database tables to have non-composite integer primary keys. Unfortunately, most of the tables I'm working with have primary keys that are either composite (i.e. the key is a combination of two or more columns), or non-integer (i.e. strings), or both.

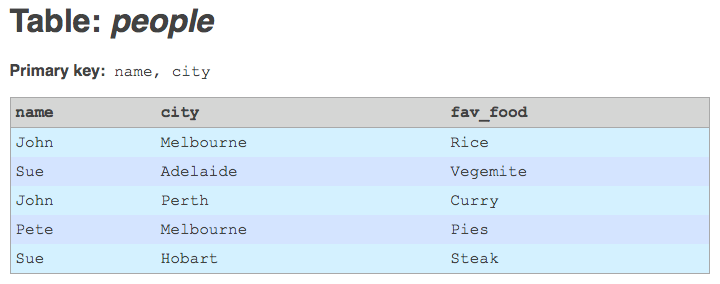
The simplest solution to this problem would be to add an auto-incrementing integer primary key column to the legacy tables. This would provide the primary key information that Migrate needs in order to do its mapping of legacy IDs to Drupal IDs. But this solution has a serious drawback. In my project, I'm going to have to re-import the legacy data at regular intervals, by deleting and re-creating all the legacy tables. And every time I do this, the auto-incrementing primary keys that get generated could be different. Records may have been deleted upstream, or new records may have been added in between other old records. Auto-increment IDs would, therefore, correspond to different composite legacy primary keys each time I re-imported the data. This would effectively make Migrate's ID mapping tables corrupt.

A better solution is needed. A solution called hashing! Here's what I've come up with:

1. Remove the legacy primary key index from the table.
2. Create a new column on the table, of type BIGINT. A MySQL BIGINT field allocates 64 bits (8 bytes) of space for each value.
3. If the primary key is composite, concatenate the columns of the primary key together (optionally separated by a delimiter).
4. Calculate the SHA1 hash of the concatenated primary key string. An SHA1 hash consists of 40 hexadecimal digits. Since each hex digit stores 2⁴ different values, each hex digit requires 4 bits of storage; therefore 40 hex digits require 160 bits of storage, which is 20 bytes.
5. Convert the numeric hash to a string.
6. Truncate the hash string down to the first 16 hex digits.
7. Convert the hash string back into a number. Each hex digit requires 4 bits of storage; therefore 16 hex digits require 64 bits of storage, which is 8 bytes.
8. Convert the number from hex (base 16) to decimal (base 10).
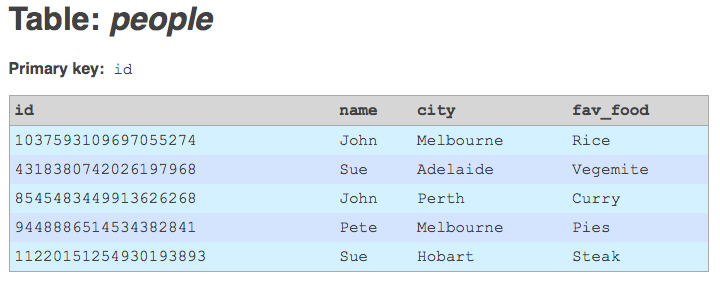
9. Store the decimal number in your new BIGINT field. You'll find that the number is conveniently just small enough to fit into this 64-bit field.
10. Now that the new BIGINT field is populated with unique values, upgrade it to a primary key field.
11. Add an index that corresponds to the legacy primary key, just to maintain lookup performance (you could make it a unique key, but that's not really necessary).

The SQL statement that lets you achieve this in MySQL looks like this:

ALTER TABLE people DROP PRIMARY KEY;
ALTER TABLE people ADD id BIGINT UNSIGNED NOT NULL FIRST;
UPDATE people SET id = CONV(SUBSTRING(CAST(SHA(CONCAT(name, ',', city)) AS CHAR), 1, 16), 16, 10);
ALTER TABLE people ADD PRIMARY KEY(id);
ALTER TABLE people ADD INDEX (name, city);

Note: you will also need to alter the relevant migrate_map_X tables in your database, and change the sourceid and destid fields in these tables to be of type BIGINT.

Hashing has a tremendous advantage over using auto-increment IDs. When you pass a given string to a hash function, it always yields the exact same hash value. Therefore, whenever you hash a given string-based primary key, it always yields the exact same integer value. And that's my problem solved: I get constant integer ID values each time I re-import my legacy data, so long as the legacy primary keys remain constant between imports.

Storing the 64-bit hash value in MySQL is straightforward enough. However, a word of caution once you continue on to the PHP level: PHP does not guarantee to have a 64-bit integer data type available. It should be present on all 64-bit machines running PHP. However, if you're still on a 32-bit processor, chances are that a 32-bit integer is the maximum integer size available to you in PHP. There's a trick where you can store an integer of up to 52 bits using PHP floats, but it's pretty dodgy, and having 64 bits guaranteed is far preferable. Thankfully, all my environments for my project (dev, staging, production) have 64-bit processors available, so I'm not too worried about this issue.

I also have yet to confirm 100% whether 16 out of 40 digits from an SHA1 hash is enough to guarantee unique IDs. In my current legacy data set, I've applied this technique to all my tables, and haven't encountered a single duplicate (I also experimented briefly with CRC32 checksums, and very quickly ran into duplicate ID issues). However, that doesn't prove anything — except that duplicate IDs are very unlikely. I'd love to hear from anyone who has hard probability figures about this: if I'm using 16 digits of a hash, what are the chances of a collision? I know that Git, for example, stores commit IDs as SHA1 hashes, and it lets you then specify commit IDs using only the first few digits of the hash (e.g. the first 7 digits is most common). However, Git makes no guarantee that a subset of the hash value is unique; and in the case of a collision, it will ask you to provide enough digits to yield a unique hash. But I've never had Git tell me that, as yet.